Numeric algorithms
sal/algo/numerics.h
| modular_pow | modular exponentiation |
| int_pow | integer exponentiation |
| fibonacci | nth fibonacci number |
| make_cyclic | create a cyclic number from 1/prime in given base |
| cyclic_length | length of cyclic number from 1/prime in given base, 0 if acyclic |
| is_pow | checks if guess is a power of base |
| is_square | checks if number is a perfect square |
| gcd | greatest common denominator (binary) |
| gcd_euclidean | Euclidean algorithm for gcd |
| gcd_alt | Another way for expressing the Euclidean algorithm |
| totient | number of integers less than n that is relatively prime with n |
| mul | matrix chain multiplication ordering |
| factorize | prime factorization of smooth numbers |
| factorize_rough | prime factorization of numbers with large prime factors |
| num_factors | total number of factors (including composites) |
| sum_factors | sum of all factors (including composites) |
Exponentiation ¶
Declaration
int modular_pow(int base, int exponent, int modulus);
int int_pow(int base, int exponent);Example
// 13789^722341 % 2345
modular_pow(13789, 722341, 2345);
// int 2029
int_pow(5, 3);
// int 125Discussion
The general approach is to exponentiate by squaring the base and
reducing the exponent to at most half each time. This gurantees completion
after Θ(lg(exponent)) computations.
Some more examples here.
Fibonacci ¶
Declaration
template <typename T>
T fibonacci(size_t n);Parameters
| n | nth fibonacci number, sequence starting: (n=0)0, 1, 1.. |
Example
fibonacci<Infint>(1000);
// Infint 43466557686937456435688527675040625802564660517371780402481729089536555417949051890403879840079255169295922593080322634775209689623239873322471161642996440906533187938298969649928516003704476137795166849228875Discussion
Since exponentiation can be done in Θ(lg(n)) time,
expanding out clever matrices also shares that time complexity.
Because the fibonacci sequence can be defined recursively as a linear
combination of previous terms, such a matrix exists (the companion matrix), and is:
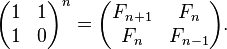
Cyclic numbers ¶
Declaration
size_t make_cyclic(int base, int prime);
size_t cyclic_length(int base, int prime);Parameters
| base | number base |
| prime | prime that does not divide base |
Example
// repeating part of 1/7 in base 10
make_cyclic(10, 7);
// size_t 142857
// length of repeating part of 1/7 in base 10
cycle_length(10, 7);
// size_t 6Discussion
Cyclic numbers are related to repeating decimals, from which they can be generated in a given base b with prime p using the relation
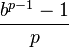
They can be constructed by computing the digits of 1/p in base b
by long division and collecting the digits.
Integer power ¶
Declaration
bool is_pow(int guess, int base);Example
is_pow(4194304,4);
// bool trueDiscussion
Through divisions, checks whether guess is an integer power of base.
Perfect square ¶
Declaration
bool is_square(long guess);Example
is_square(21489798124);
// bool falseDiscussion
Used in tight loops of many number theory problems. Algorithm is written by maartinus from stackoverflow.
Greatest Common Denominator ¶
Declaration
unsigned int gcd(int a, int b);
unsigned int gcd_euclidean(int a, int b);
unsigned int gcd_alt(int a, int b);Parameters
| a | integer (can be negative) |
| b | integer (can be negative) |
Example
gcd(56, 91);
// unsigned int 7Discussion
Often used to solve combination problems. The binary optimization is used because gcd's common usage in time critical operations. The alternative versions are much simpler and easier to memorize.
Euler's Totient ¶
Declaration
unsigned long long totient(unsigned long long n);
auto phi = totient;Parameters
| n | number to find the totient of |
Example
totient(500);
// unsigned long long 200Discussion
Number of positive integers less than n that is relatively prime to n.
1 < k < n such that gcd(k,n) == 1
It is multiplicative, so
phi(a*b) == phi(a) * phi(b)
One application is in Euler's theorem: that a and n are relatively prime iff
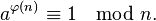
With applications here.
Matrix Chain Multiplication ¶
Declaration
template <typename Indexable>
typename Indexable::value_type mul(const Indexable& items);
// specialization for matrices
Matrix<T> mul(const Indexable& mats);Example
std::vector<Matrix<int>> mats;
size_t row {30}, col {35};
for (int i = 0; i != 100; ++i) {
// generate sequence of random matrices
mats.push_back(random_matrix<int>(row, col, 0, 50));
// next matrix's row must be prev matrix's col
row = col;
col = rand() % 100 + 5; // between 5 - 105
}
mul(mats);
// Matrix<int> Discussion
Θ(n^3) work is done optimally parenthesize the multiplications using dynamic programming.
This order affects the number of operations required; using Wikipedia's example:
suppose A is a 10 × 30 matrix, B is a 30 × 5 matrix, and C is a 5 × 60 matrix. Then,
(AB)C = (10×30×5) + (10×5×60) = 1500 + 3000 = 4500 operations
A(BC) = (30×5×60) + (10×30×60) = 9000 + 18000 = 27000 operations.
Integer Factorization ¶
Declaration
template <typename T>
std::vector<T> factorize(T num);
template <typename T>
std::vector<T> factorize_rough(T num);
size_t num_factors(size_t num);
size_t sum_factors(size_t num);Example
size_t num = 421412;
factorize(421412);
// vector<size_t> 2 2 137 769 (in order)
num_factors(num);
// size_t 12 (1 2 4 137 274 548 769 1538 3076 105353 210706 421412)
sum_factors(num);
// size_t 743820 (1 + 2 + 4 + 137 + ... + 421412)
// factorize primes or semiprimes
big_int semiprime = 32452843 * 32452867; // 1053187797650881
// would still not be too slow
factorize(semiprime);
// would be faster
factorize_rough(semiprime);
/* would be much faster for repeated uses (primes are kept static) */Discussion
Factorizing in polynomial time is still an open problem.
Smooth numbers are ones that have small prime factors,
while rough numbers factor into large primes.
Trial division is used to factorize both, with the difference being
the divisor sequence for smooth numbers being that of odd numbers (2, 3, 5, 7, 9,...), while
rough numbers is that of generated primes (2, 3, 5, 7, 11,...). Trial division is very fast
for practical encounters.